Basic friction

In physicsland, there are two kinds of friction, kinetic and static, and both are considered Coulomb friction, this Wikipedia article goes into way more detail than this page, but the main assumptions to solve problems in a physics class are

the friction force ( f) is proportional to the normal force, with a constant µ, so that f = N*µ
the friction force is perpendicular to the direction of the normal force
kinetic friction (subscript k) points opposite the direction of the velocity
Static friction (subscript s) points opposite the sum of the rest of the forces
Static friction balances whatever the net force would be without it, up to a maximum. Whenever a question is asking about a minimum or maximum, it usually means the conditions that cause max static friction.

Below, is a plot of the magnitude of the friction force(y-axis blue) acting on a block on the ground being pushed with increasing force (x-axis). the force is equal to the applied force until it reaches the maximum static friction. A slight increase beyond that imbalances the forces causing the block to move, and the coefficient of friction drops to the kinetic value, further imbalanceing the forces, causing a sharp jump in acceleration. After it "breaks free" the kinetic friction stays at a fixed value until something causes it to come to a complete stop. If the applied force disappears, the kinetic friction will slow it to a stop; once it stops, the force is zero, as friction does not have anything to resist.

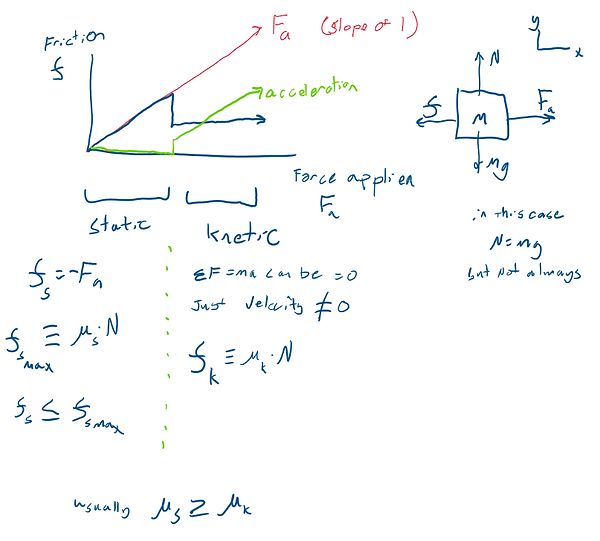
In real life, there are more kinds of friction than the two detailed here, forces like air resistance and viscous drag are proportional to the velocity between the surfaces. An introductory physics class might have you calculate drag on a skydiver, but from there getting to how their velocity changes with time, requires solving differential equations, which is usually beyond the scope of your class.

A common problem just above the basic level involves pushing the block at an angle, sometimes drawn as a person pushing downward on a box from behind, or pulling up from the front. These are mathematically the same problem. The normal force is whatever is required to balance (a_y = 0, its not going up) gravity and the y component of the applied force (be careful with sign flips here)

Common unknowns

acceleration, given mu, angle, and mass. Solve for normal force with F_y = ma_y = 0, then find friction to find net force
Force required to overcome friction, given acceleration (sometimes zero), mass, mu and angle. The same process as above
Maximum pushing angle, given applied force, mass, mu, starting from rest. Pushing forward is more than the max static friction, but pushing down is not useful, at some point, there is a maximum angle where it can break free. It's hard to do this one with numbers only, try keeping everything (including knows) as variables.
Slip angle. the same process as above with no applied force, proved below, tan(theta) = mu OR cot(theta) = mu depending on reference angle