Work Energy Block on a slope
A static forces approach is the best way to handle simple situations where nothing is moving, but integrating forces to find changes in position and velocity is sometimes much more complicated. The work-energy method can be used to solve significantly more complex systems with less effort. Starting with a simple example, a block on a slope has an easy free-body diagram that doesn't change with position giving a constant acceleration as found in this example problem. Constant acceleration can be used with the kinematic equations to find a final speed after a given time or displacement. If the problem asks for the velocity after some displacement (for example, the bottom of the slope), the work-energy method is far simpler.
The image below shows a possible setup of the FBD used for the kinematics approach with an applied force, friction, gravity, and normal force. The same setup is used for the W-E method.
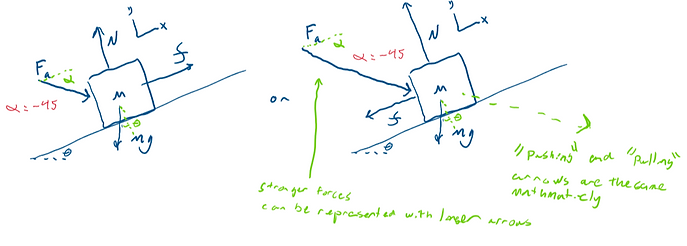
Below, the same situation is shown as a work energy diagram. It's best to draw both states of the system so that the energy equation can be made from the information in the drawings. The most important information to show is the path taken, height change, and what external forces apply. Technically a coordinate system is not needed (except for knowing the direction of gravity) but is helpful in some more complicated problems.
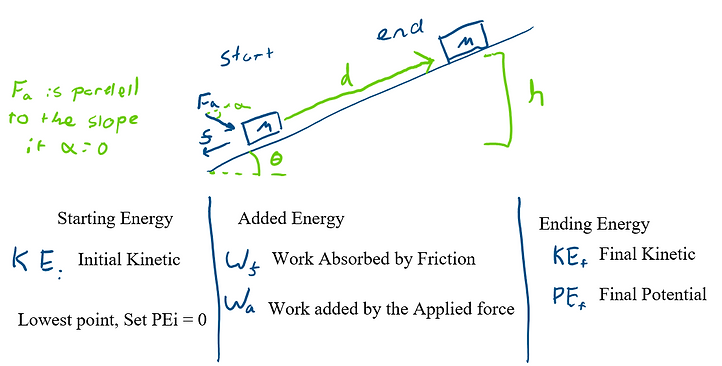
Then by finding the types of energy at each state and any added energy, the work equation can be found. Next, each term can be filled out into each formula.

Now plug in what's known, and other relationships like the length and angle of the slope to the height. Then solve for the unknown variable.

Jumping to a related problem, if there are multiple points on a path the energies at each point can be set equal to each other by setting it up as (Initial energy) = (energy at a point) - (work added so far). This allows you to solve for the velocity at many points while only setting up the equations once. For example below, this no-friction roller coaster starts from rest at the top and rolls through a loop, then reaches the bottom at a high speed before being stopped by a large spring. In order to solve for the velocity at each state, the only thing needed is the change in height from the start to the current position and gravity.
